LMS和RLS算法的性能对比
1. 仿真模型
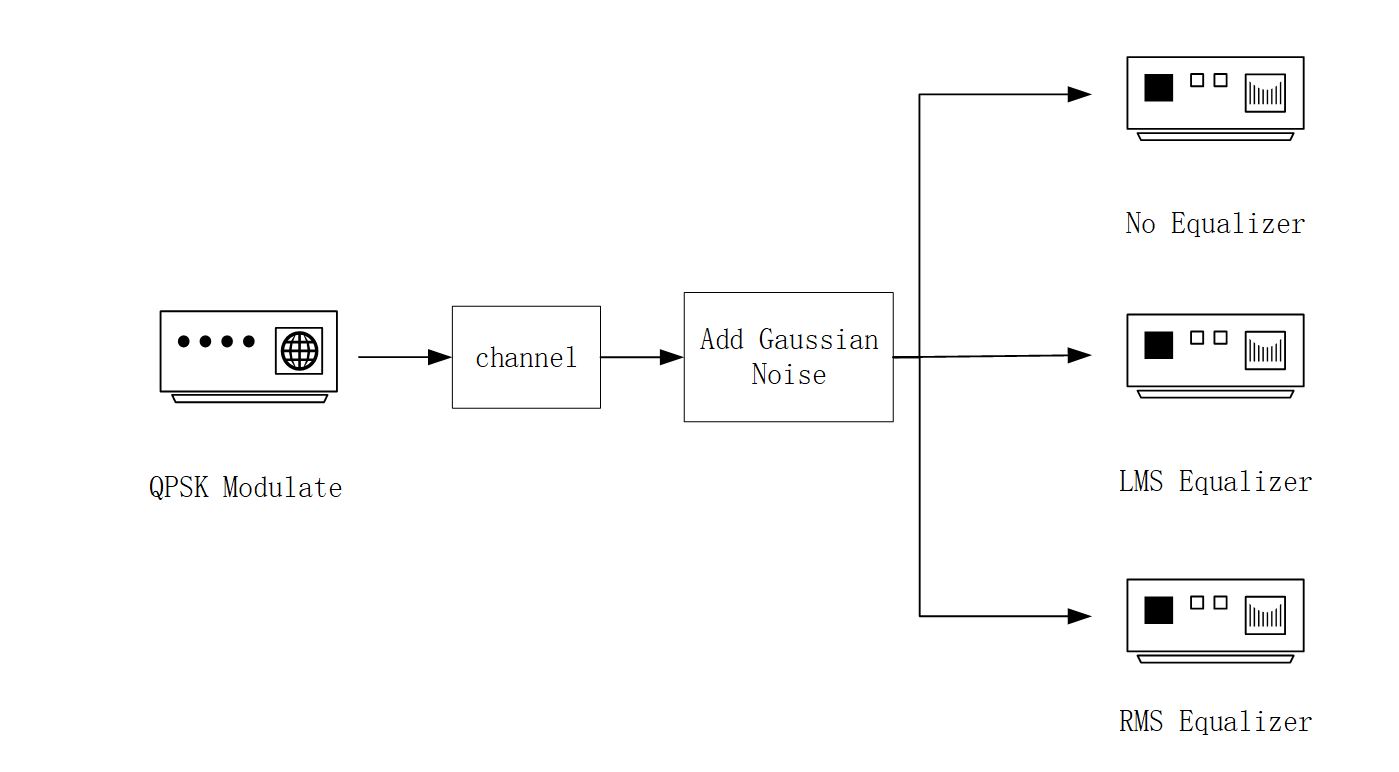
图一、水声通信仿真模型
2. 调制方式及信道设置
要求:调制方式QPSK、序列长度2048、训练序列长度1024、信噪比范围5-20dB,比较LMS和RLS算法的性能,均衡后的均方误差。
2.1调制方式设置
采用QPSK调制方式,二进制序列长度为2048,二进制转QPSK信号对应如下:
2.2信道设置
根据要求信道设置如下:
H=[1;0;0;0;0.4;0;0;0.2];
可以通过卷积得到调制信号通过信道以后的信号具体如下:
Y=filter(H,1,X);
该信道的冲激响应和阶跃响应为。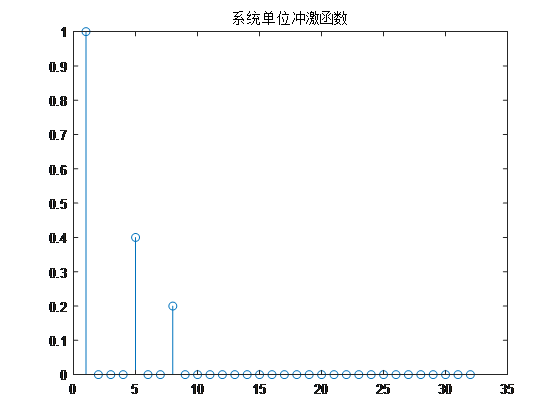
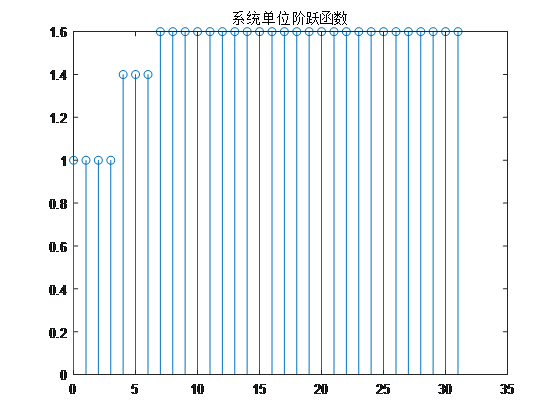
图二、信道的冲击响应和阶跃响应
2.3. LMS和RMS滤波器
自适应滤波,就是利用前一时刻以获得的滤波器参数的结果,自动的调节现时刻的滤波器参数,以适应信号和噪声未知的或随时间变化的统计特性,从而实现最优滤波。
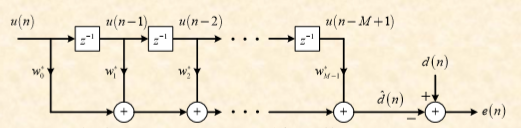
图三、M个抽头系数的横向滤波器最优权向量
2.3.1 最小均方(LMS)自适应滤波器
LMS
自适应算法是一种特殊的梯度估计,不必重复使用数据,也不必对相关矩阵和互相关矩阵进行运算,只需要在每次迭代时利用输入向量和期望响应,结构简单,易于实现。但LMS
收敛速度较慢。
LMS
算法的四个性能:一、收敛性;二、收敛速度;三、稳态误差;四、计算复杂度。只有在输入信号具有严格稳定的统计特性时,权向量的优解是不变的。否则,将会随着统计特性的变化而变化。
通过不断调整滤波器的抽头系数,使得权重接近优解。因此自适应算法在平稳条件下的性能表现可以认为是非平稳条件下的一种特殊情况。
2.3.2递推最小二乘(RLS)滤波器
该算法根据有限个观测数据获取最优解,求出如下图所示的M个抽头系数的横向滤波器最优权向量。递归最小二乘(RLS)算法用迭代算法代替矩阵求逆达到降低运算量的目的。
3. 仿真结果
3.1. QPSK复数调制和载波调制在RLS、LMS,不同信噪比下的均方误差:
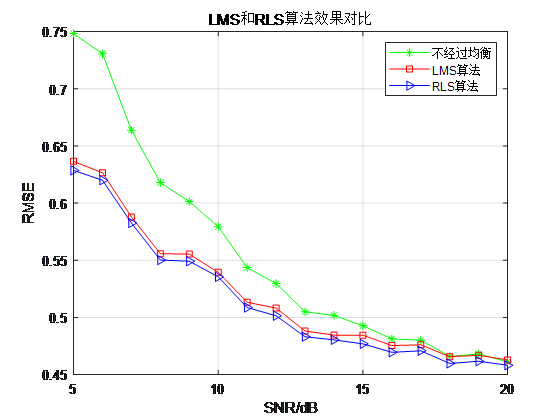

复数调制通过RMS、LMS均方误差 b. 载波调制通过RMS、LMS均方误差
复数调制、载波调制在 [5,20]噪声强度下的平均误码率对比
| 复数调制 | 载波调制 | |
|---|---|---|
| 不经过均衡 | 0.5544 | 0.4124 |
| LMS算法 | 0.5205 | 0.3872 |
| RMS算法 | 0.5148 | 0.3820 |
分析:
1、QPSK复数调制后通过RLS算法相比LMS算法、不经过均衡,均方误差分别降低1.10%、7.14%。
2、QPSK载波调制后通过RLS算法相比LMS算法、不经过均衡,均方误差分别降低1.26%、7.37%。
3、RMS算法的均方误差优于LMS算法的均方误差优于不经过均衡。
通过仿真结果可以看出,均方误差随着信噪比的升高而降低,与理论计算值相符。
结论:
在QPSK信号调制中RMS算法性能优于LMS算法性能,即RMS算法均衡后的均方误差小于LMS算法均衡后的均方误差。
- 本文链接:http://www.codekp.cn/2020/12/04/%E6%B0%B4%E5%A3%B0%E9%80%9A%E4%BF%A1%E8%AF%BE%E7%A8%8B%E4%BD%9C%E4%B8%9A%E4%B8%9A-%E4%BA%8C/
- 版权声明:本博客所有文章除特别声明外,均默认采用 许可协议。
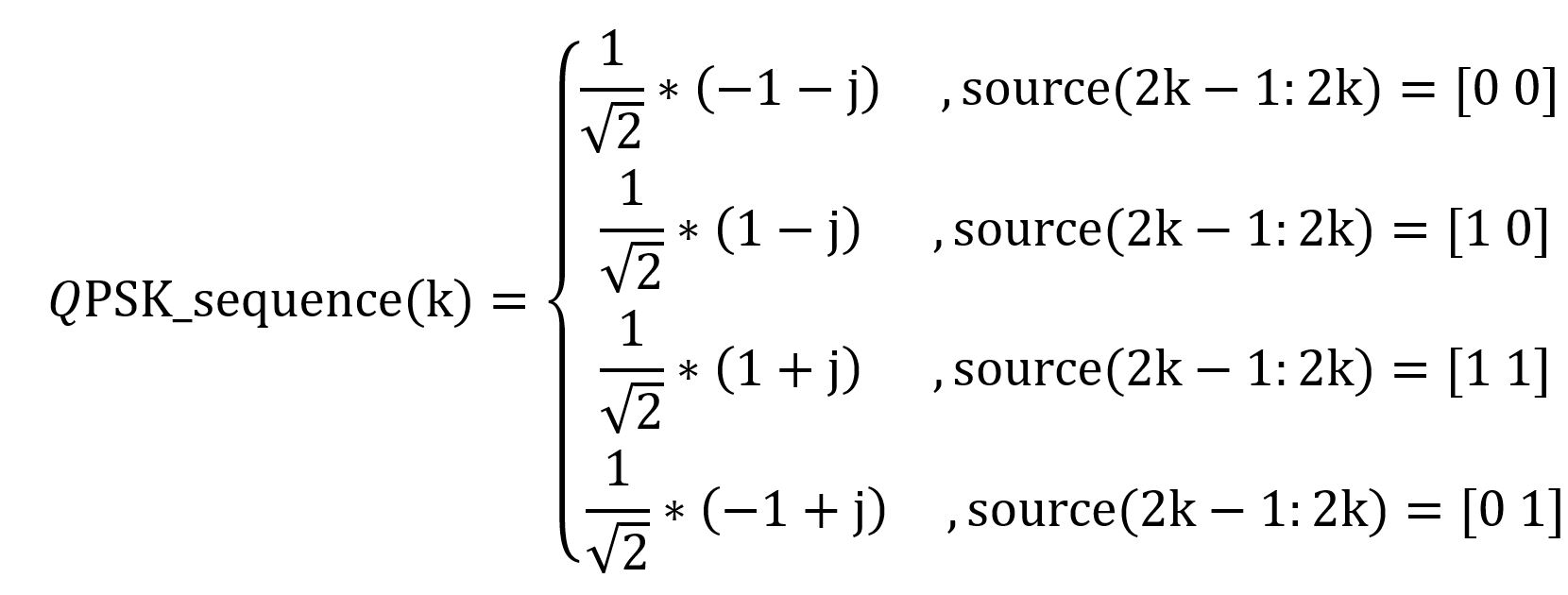



您可以点击下方按钮切换对应评论系统。
GitHub Issues